Difference between revisions of "Pair Trading Models"
(→Orthogonal Model) |
|||
| Line 213: | Line 213: | ||
(section still under construction) | (section still under construction) | ||
| + | |||
| + | '''This model is experimental.''' | ||
| + | |||
| + | == Kalman-grid Model == | ||
| + | This model follows up the Kalman model and it tries to fix its biggest flaw - sensitivity to δ parameter. How? By executing '''whole grid''' of Kalman filters with different δ settings at the same time. | ||
| + | |||
| + | Then it evaluates separate backtests of underlying Kalman strategies and from their measures it creates weights for calculating α, β and standard deviation. This process goes on incrementally (at each price observation!). | ||
| + | |||
| + | (under construction) | ||
| + | |||
| + | === Model Support === | ||
| + | * in PTL backtester: '''yes''' (max Z-score not supported) | ||
| + | * in PTL portfolio backtester: '''not yet''' | ||
| + | * in PTL Trader: '''not yet''' | ||
| + | |||
| + | === Model Neutrality === | ||
| + | For Kalman Model, we support both '''dollar neutral''' (equal dollar amount invested to each leg) and '''beta neutral''' regimes. | ||
| + | |||
| + | === Model Parameters === | ||
| + | * Kalman filter observation covariance V<sub>e</sub>, typical value is 0.001 | ||
| + | |||
'''This model is experimental.''' | '''This model is experimental.''' | ||
Revision as of 14:42, 12 February 2015
Pair Trading Lab offers pair trading algorithms based on various mathematical models. These are models currently supported in PTL:
Contents |
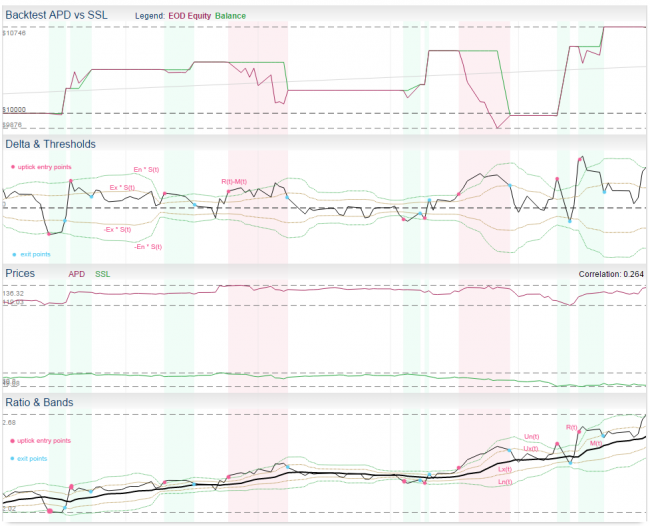
Ratio Model
This is one of the standard pair trading models described in literature. It is based in ratio of instrument prices, moving average and standard deviation. In other words, it is based on Bollinger Bands indicator.
Since Nov 27th 2014, this model also supports additional RSI filter you can use in addition to Bollinger Bands method.
Model Support
- in PTL backtester: yes (max Z-score not supported)
- in PTL portfolio backtester: yes
- in PTL Trader: yes (RSI supported since v1.2.0)
Model Neutrality
We currently support only dollar-neutral version of this model, which means we allocate same amounts of margin to both legs based on current prices at the time of opening the position.
Model Parameters
- entry threshold En for Z-score, typical value range is <1.5, 2.5>, 2.0 is used most often
- exit threshold Ex for Z-score, typical value is <-0.5, 0.5>, 0 is used most often...we allow positive values only for now
- max Z-score Emax (optional, to filter out extremes, typical value is >4 if used)
- moving average period Pm (typical range <10, 100>), default = 15
- moving average type T (algorithm), default = exponential
- standard deviation period Ps (typical range <10, 100>), default = 15
- entry mode (simple, uptick, downtick)
- RSI period and threshold (optional RSI filtering)
Description
- we trade pair of stocks A, B, having price series A(t), B(t)
- we need to calculate ratio time series R(t) = A(t) / B(t)
- let's apply moving average of type T with period Pm on R(t) to get time series M(t)
- let's apply standard deviation with period Ps on R(t) to get time series S(t)
- now we can create Z-score series Z(t) as Z(t) = (R(t) - M(t)) / S(t), this time series can give us z-score to signal trading decision directly
- another common approach (to visualize) is to create bands and put it above the moving average M(t):
- upper entry band Un(t) = M(t) + S(t) * En
- lower entry band Ln(t) = M(t) - S(t) * En
- upper exit band Ux(t) = M(t) + S(t) * Ex
- lower exit band Lx(t) = M(t) - S(t) * Ex
- these bands are actually the same bands as in Bollinger Bands indicator and we can use crossing of R(t) and bands as trade signals
Entering Position
There are certain possible approaches how to interpret model statistics in order to make trading decisions. For entering position, we used to call them entry modes. This is the list of them and description how they work:
- entry mode = simple:
- to open short pair position, it is simple enough if the Z-score Z(t) >= En (equivalent to R(t) >= Un(t))
- to open long pair position, it is simple enough if the Z-score Z(t) <= -En (equivalent to R(t) <= Ln(t))
- entry mode = uptick: same as simple, but in addition, previous Z-score must be below the entry band (so we cross the band from inside to outside):
- to open short pair position, we require Z(t) >= En (equivalent to R(t) >= Un(t)) and Z(t-1) < En (same as R(t-1) < Un(t-1))
- to open long pair position, we require Z(t) <= -En (equivalent to R(t) <= Ln(t)) and Z(t-1) > -En (same as R(t-1) > Ln(t-1))
- entry mode = downtick: we wait for the Z-score crossing back the band from outside to inside:
- to open short pair position, we require Z(t) < En and Z(t-1) >= En and Z(t) > Ex
- when using bands, it is the same as having R(t) < Un(t) and R(t-1) >= Un(t-1) and R(t) > Ux(t)
- to open long pair position, we require Z(t) > -En and Z(t-1) <= -En and Z(t) < -Ex
- when using bands, it is the same as having R(t) > Ln(t) and R(t-1) <= Ln(t-1) and R(t) < Lx(t)
Why do we have the simple entry mode? In normal situations and backtests, it gives same results as the uptick mode. But the difference comes up while trading multiple pairs in portfolio. The simple mode allows you to jump in the position immediately after a new slot is freed, regardless of the previous Z-scores.
Which entry mode is better? Hard to tell, sometimes the uptick, sometimes the downtick. You have to do your homework and decide, which idea suits your trading style better. In general, uptick/simple mode is more aggressive, as it does not wait for first signs of spread mean reversion.
Exiting Position
For exiting position, we always use only these simple rules:
- we exit short position when Z(t) <= Ex (equivalent to R(t) <= Ux(t))
- we exit long position when Z(t) >= -Ex (equivalent to R(t) >= Lx(t))
Moving Average Types
You can choose from these moving average algorithms:
- Simple Moving Average (SMA)
- Exponential Moving Average (EMA)
- Weighted Moving Average (WMA)
- Double Exponential Moving Average (DEMA)
- Triple Exponential Moving Average (TEMA)
- Triangular Moving Average (TMA)
- Kaufman Adaptive Moving Average (KAMA)
- MESA Adaptive Moving Average (MAMA)
- Triple Exponential T3 Moving Average
Which one is the best? It depends, you have to test for yourself. They mostly differ in the term of memory and how fast they react to changes. Industry standard and the default is EMA. We suggest to try all of them on some sample pair to see how they work.
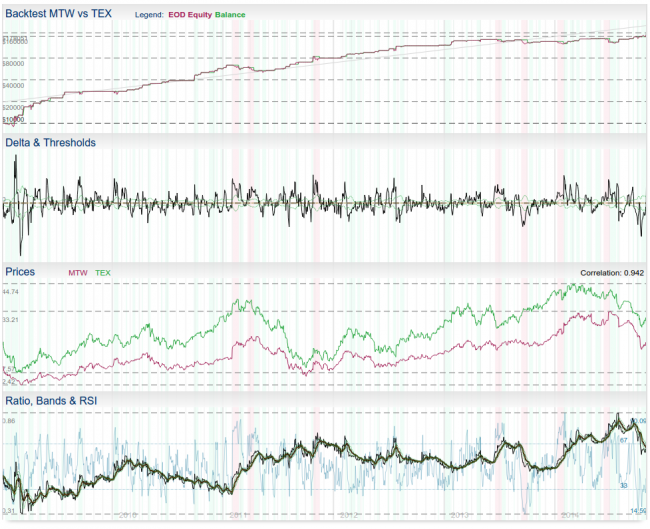
RSI Filtering
You can combine the Z-score/Bollinger Band model with RSI indicator applied on the ratio R(t). RSI filter will be automatically enabled if you set RSI threshold to other value than zero. RSI filter is combined with the Z-score rules using AND operator (both entry rule and RSI entry rule must be true to open a position).
You can also change the RSI period if you want (default period = 15).
RSI Threshold is value between 0 and 50. Because RSI indicator value oscillates between 0 and 100 (where 50 = mean), your threshold value is just used to set real thresholds for RSI:
- let's assume RSI Period Pr was entered
- effective RSI value threshold is then 50+Pr (upper) and 50-Pr (lower)
- you can see both thresholds in the example image at the right side
Example:
- RSI Threshold entered is 15
- then, short positions are only opened, if RSI >= 65 (50+15)
- long positions are only opened, if RSI <=35 (50-15)
Useful hint: if you want to control entry rules just by RSI, you can set Entry Mode to simple and Entry Threshold to some low value.
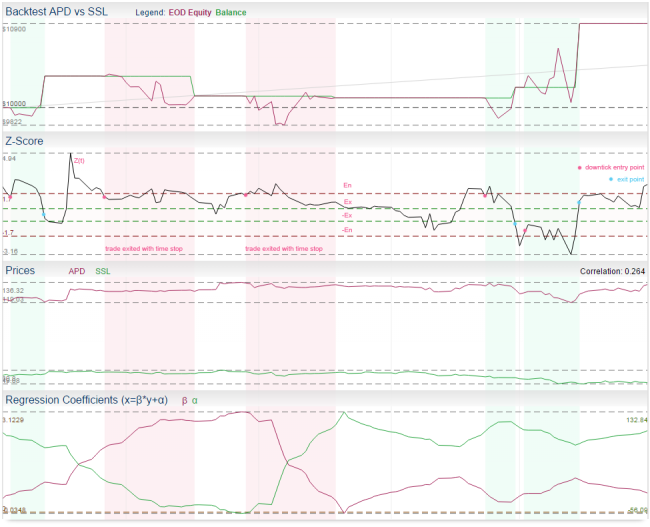
Residual Model
Residual mode is based on linear regression. In literature it has been also referred to as the cointegration approach. Linear regression of both stocks is constructed in order to fit a linear relationship between both instruments and estimate its best parameters using the OLS method (Ordinary Least Squares). Then, standard deviation is applied on the regression residuals to estimate its statistical properties and calculate Z-scores.
This particular implementation is very simple. The regression is constructed using floating window of a fixed period, the same period is used for calculating the standard deviation.
Model Support
- in PTL backtester: yes (max Z-score not supported)
- in PTL portfolio backtester: yes
- in PTL Trader: yes (uptick and downtick modes are supported since v1.2.0)
Model Neutrality
We currently support only dollar-neutral version of this model, which means we allocate same amounts of margin to both legs based on current prices at the time of opening the position.
Model Parameters
- entry threshold En for Z-score, typical value range is <1.2, 2.5>, 1.5 is used most often
- exit threshold Ex for Z-score, typical value is <-0.5, 0.5>, 0 is used most often...we allow positive values only for now
- max Z-score Emax (optional, to filter out extremes, typical value is >4 if used)
- linear regression period P (floating window is used), typical range <15, 300>
- entry mode (simple, uptick, downtick)
Description
- we trade pair of stocks A, B, having price series A(t), B(t)
- first we need to construct a linear regression between A(t), B(t) using OLS, where A(t) = β * B(t) + α + R(t)
- because we use floating window of period P (we calculate new regression each day), we actually get new series β(t), α(t), R(t), where β(t), α(t) are series of regression coefficients and R(t) are residuals (prediction errors)
- R(t) = A(t) - (β(t) * B(t) + α(t))
- then we apply standard deviation of period P on residuals R(t) and we put it to S(t)
- now we can create Z-score series Z(t) as Z(t) = R(t) / S(t), this time series can give us z-score to signal trading decision directly
Entering Position
There are certain possible approaches how to interpret model statistics in order to make trading decisions. For entering position, we used to call them entry modes. This is the list of them and description how they work:
- entry mode = simple:
- to open short pair position, it is simple enough if the Z-score Z(t) >= En
- to open long pair position, it is simple enough if the Z-score Z(t) <= -En
- entry mode = uptick: same as simple, but in addition, previous Z-score must be below the entry band (so we cross the band from inside to outside):
- to open short pair position, we require Z(t) >= En and Z(t-1) < En
- to open long pair position, we require Z(t) <= -En and Z(t-1) > -En
- entry mode = downtick: we wait for the Z-score crossing back the band from outside to inside:
- to open short pair position, we require Z(t) < En and Z(t-1) >= En and Z(t) > Ex
- to open long pair position, we require Z(t) > -En and Z(t-1) <= -En and Z(t) < -Ex
Exiting Position
For exiting position, we always use only these simple rules:
- we exit short position when Z(t) <= Ex
- we exit long position when Z(t) >= -Ex
Orthogonal Model
This model is similar to Residual model, but it uses orthogonal regression/total least squares instead of OLS. In addition, it has some extra features. Linear regression of both stocks is constructed in order to fit a linear relationship between both instruments and estimate its best parameters using the TLS method (Total Least Squares). Then, standard deviation is applied on the regression residuals to estimate its statistical properties and calculate Z-scores.
The regression is constructed using floating window of a fixed period. Standard deviation indicator is then applied to regression residuals (it can have a different period).
Model Support
- in PTL backtester: yes (max Z-score not supported)
- in PTL portfolio backtester: no
- in PTL Trader: no
Model Neutrality
We support both dollar neutral (equal dollar amount invested to each leg) and beta neutral regimes. In beta neutral mode, we determine the hedge ratio from TLS regression too, but using significantly longer floating period (240 or more).
Model Parameters
- entry threshold En for Z-score, typical value range is <1.2, 2.5>, 1.5 is used most often
- entry threshold End for Z-score, typical value range is slightly less than En - used as another band for downtick mode only
- exit threshold Ex for Z-score, typical value is <-0.5, 0.5>, 0 is used most often...we allow positive values only for now
- max Z-score Emax (optional, to filter out extremes, typical value is >4 if used)
- linear regression period P (floating window is used), typical range <50, 300>
- standard deviation period, typical range <25, 100>
- entry mode (simple, uptick, downtick)
(section still under construction)
Important: TLS is numerically far less stable than OLS, especially for floating-window case with short periods. For this model, you should use periods of 40 or more. But even in case that TLS provides unstable results (you can see it as spikes in β), residuals are still stable.
Description
- see the math behind the regression itself here (Deming regression is a 2D case of TLS)
- from the regression, we get coefficients β, α and orthogonal residuals R(t)
- then we apply standard deviation of period P on residuals R(t) and we put it to S(t)
- now we can create Z-score series Z(t) as Z(t) = R(t) / S(t), this time series can give us z-score to signal trading decision directly
Entering Position
There are certain possible approaches how to interpret model statistics in order to make trading decisions. For entering position, we used to call them entry modes. This is the list of them and description how they work:
- entry mode = simple:
- to open short pair position, it is simple enough if the Z-score Z(t) >= En
- to open long pair position, it is simple enough if the Z-score Z(t) <= -En
- entry mode = uptick: same as simple, but in addition, previous Z-score must be below the entry band (so we cross the band from inside to outside):
- to open short pair position, we require Z(t) >= En and Z(t-1) < En
- to open long pair position, we require Z(t) <= -En and Z(t-1) > -En
- entry mode = downtick: we wait for the Z-score crossing back the band from outside to inside:
- to open short pair position, we require Z(t) < En and Z(t-1) >= En and Z(t) > End
- to open long pair position, we require Z(t) > -En and Z(t-1) <= -En and Z(t) < -End
Exiting Position
For exiting position, we always use only these simple rules:
- we exit short position when Z(t) <= Ex
- we exit long position when Z(t) >= -Ex
This model is experimental.
Kalman Model
This model is based on Kalman Filter. In this case, the filter is used here instead of linear regression to determine proper hedge ratio, deviation from the mean and the standard deviation of the spread. The advantage is that this filter is superior when dealing with noise compared to OLS or TLS methods, also it does not have any lookback period to optimize. The disadvantage is that is has another parameters (like δ) to find out.
We strongly recommend to read more details about Kalman filter applications in pair trading in this book.
While Kalman Filter also estimates the standard deviation on the fly, our implementation also supports a possibility of having an auxiliary standard deviation indicator applied directly on the forecast error time series. The advantage is that you get less sensitivity on the δ parameter, but on the other hand a new lookback parameter is introduced.
Model Support
- in PTL backtester: yes (max Z-score not supported)
- in PTL portfolio backtester: not yet
- in PTL Trader: not yet
Model Neutrality
For Kalman Model, we support both dollar neutral (equal dollar amount invested to each leg) and beta neutral regimes.
Model Parameters
- Kalman filter transition covariance δ, typical value is 0.0001 - unfortunately this model is very sensitive to this parameter especially when using standard deviation estimate coming from the Kalman filter itself
- Kalman filter observation covariance Ve, typical value is 0.001
- Auxiliary standard deviation period - if equal to zero, Kalman filter is used to estimate standard deviation, if non-zero, auxiliary standard deviation indicator with this period is used (an the estimate from Kalman filter is ignored)
- Unstable period = how many Kalman filter observations are ignored at the beginning (first observations are quite unstable)
(section still under construction)
This model is experimental.
Kalman-grid Model
This model follows up the Kalman model and it tries to fix its biggest flaw - sensitivity to δ parameter. How? By executing whole grid of Kalman filters with different δ settings at the same time.
Then it evaluates separate backtests of underlying Kalman strategies and from their measures it creates weights for calculating α, β and standard deviation. This process goes on incrementally (at each price observation!).
(under construction)
Model Support
- in PTL backtester: yes (max Z-score not supported)
- in PTL portfolio backtester: not yet
- in PTL Trader: not yet
Model Neutrality
For Kalman Model, we support both dollar neutral (equal dollar amount invested to each leg) and beta neutral regimes.
Model Parameters
- Kalman filter observation covariance Ve, typical value is 0.001
This model is experimental.